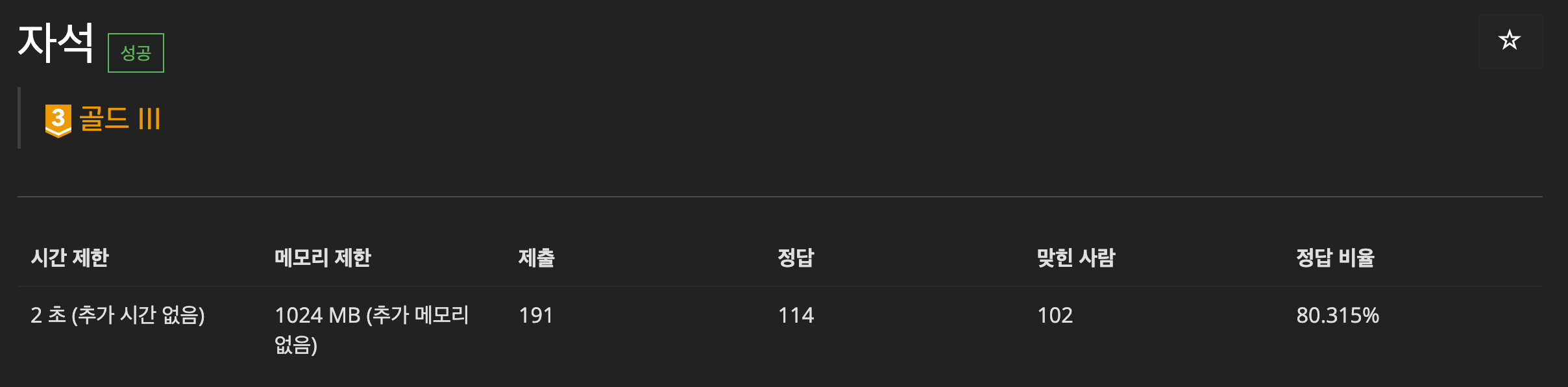
BOJ 28303 - 자석

BOJ 28303 - 자석

구간합으로 볼 때, $a_i-a_j-(i-j)K$ 의 최댓값을 찾아야하므로

$a_i-iK$ 라는 값과 $-a_j+jK$ 라는 값을 따로 관리하면 된다.

이전까지 나온 $j$중 $-a_j+jK$ 가 가장 큰 것을 $a_i-iK$ 에 더해주는 것으로 이 연산의 최댓값을 쉽게 구할 수 있다.

void solve() {
   int n, k;
   cin >> n >> k;
   vi a(n);
   fv(a);

   int ans = -2e18;
   for (int it = 0; it < 2; it++) {
      // a[i] - a[j] - (i-j)*K
      // a[i] - i * K - (a[j] - j * K)

      int mn = a[0];
      for (int i = 1; i < n; i++) {
         maxa(ans, a[i] - i * k - mn);
         mina(mn, a[i] - i * k);
      }
      reverse(all(a));
   }
   cout << ans;
}