BOJ 2569 - 짐정리

BOJ 2569 - 짐정리

참고로 이걸 푸는 방법은 O(N) 이며 따라서 다른 N = 100,000 정도 되는 문제도 토씨하나 안틀리고 4연콤을 할 수가 있다.

permutation cycle group 이 하나 있다고 생각해보자.

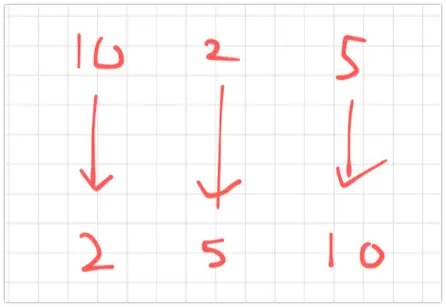
사이클 표현법으로 (10, 2, 5) 가 되는 사이클이다.

문제에서 비용을 계산하는 법을 잘 보면 나머지는 한번씩만 쓰고 가장 낮은 숫자로만 이동하는게 가장 효과적으로 보인다.​

일단 이것부터 생각해보자. 가장 작은 숫자를 한번씩 껴서 싸이클내의 모든 숫자들을 옮길 수 있을까?

항상 가능하다.

그렇지 않다고 하자. 크기 $S$를 가진 싸이클 $C$의 가장 작은 숫자 $c$ 가 그 다음으로 이동하면서 $S - 1$ 번의 이동 으로 모든 수가 제자리를 찾아가기 전에 자기 자리($c$가 원래 가야할 자리)로 간다고 하자.

그럼 $C$가 사이클이란 것에 모순이다. 따라서 항상 가능하다.

그러면 이제 그런식으로 이동을 하는게 최적이므로

총 이동 값은 $c(S-1)+\text{SUM}(C) - c$ 이다.

그런데 한가지 다른 경우가 있다.​

바로 싸이클 내부엔 없지만 싸이클 외부에 있는 가장 작은 수를 하나 빌려와서 그 수를 기준으로 싸이클들의 수가 제자리를 찾게 해주는 것이다.

예시를 들어 보자. 1이라는 수를 잠시 빌려온다고 해보자.

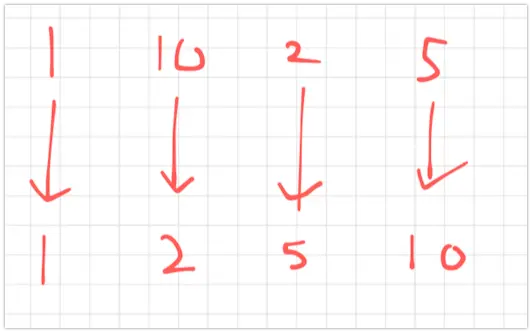
이제 이걸 $c’$ 이라고 하고, 원래 $C$ 내의 가장 작은 수(2) 를 $c$ 라고 하자.

처음에는 당연히 $c$와 $c’$ 를 교체해주는게 이득이다.

$c$ 는 다시 사이클 내부로 마지막에 가져와져야 하기 때문이다.

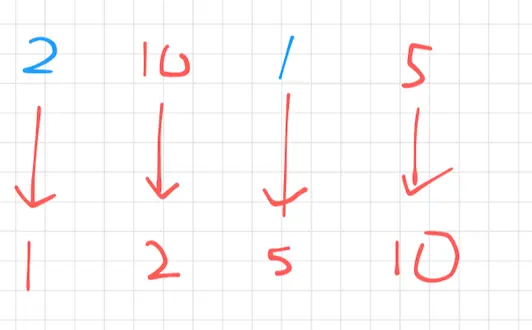
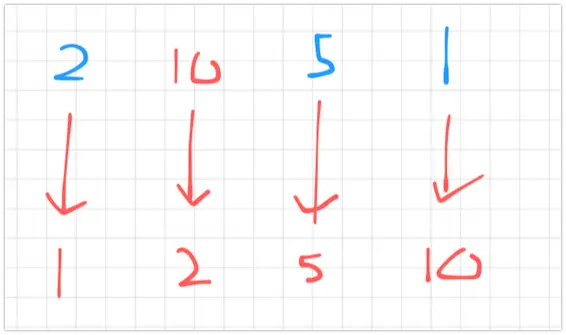
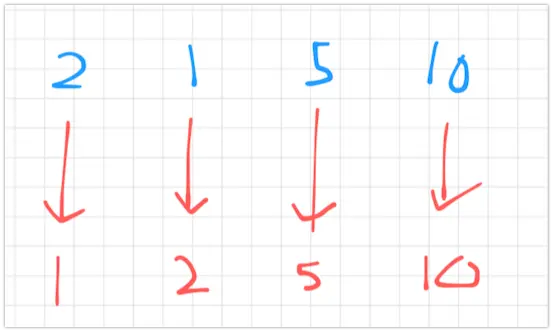
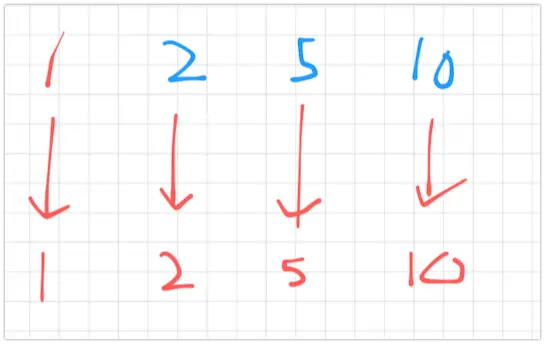
총 S + 1 번의 이동으로 가능하다.

그래서 원래 처럼 싸이클 내부의 수로만 $S - 1$ 번만에 이동하는 경우와, 싸이클 외부에서 가장 작은 수를 하나 빌려와서 $S + 1$ 번만에 정려하는 두 가지중 작은 것을 정답에 더해준다.

int main()
{
    int N, i, j; long long sum=0, m, X;
    scanf("%d", &N);
    int Pack[N][2]; vector<int> Vis(N);
    for(i=0; i<N; i++){ scanf("%d", &Pack[i][1]); Pack[i][0] = i; }
    qsort(Pack, N, sizeof(Pack[0]), Comp); m=Pack[0][1];
    for(i=0; i<N; i++){
        vector<int> Cycle; j=i;
        if(Vis[i]) continue;
        while(!Vis[j]){
            Cycle.push_back(Pack[j][1]);
            Vis[j]=1; j=Pack[j][0]; 
        }
        if(Cycle.size()<=1) continue;
        for(j=1; j<Cycle.size(); j++) sum += Cycle[0]+Cycle[j]; 
        X = (Cycle[0]-m)*(Cycle.size()-1) - 2*(Cycle[0]+m);
        if(X > 0) sum -= X;
    }
    printf("%lld\n", sum);
    return 0;
}