BOJ 24726 - 미적분학 입문하기 2

BOJ 24726 - 미적분학 입문하기 2

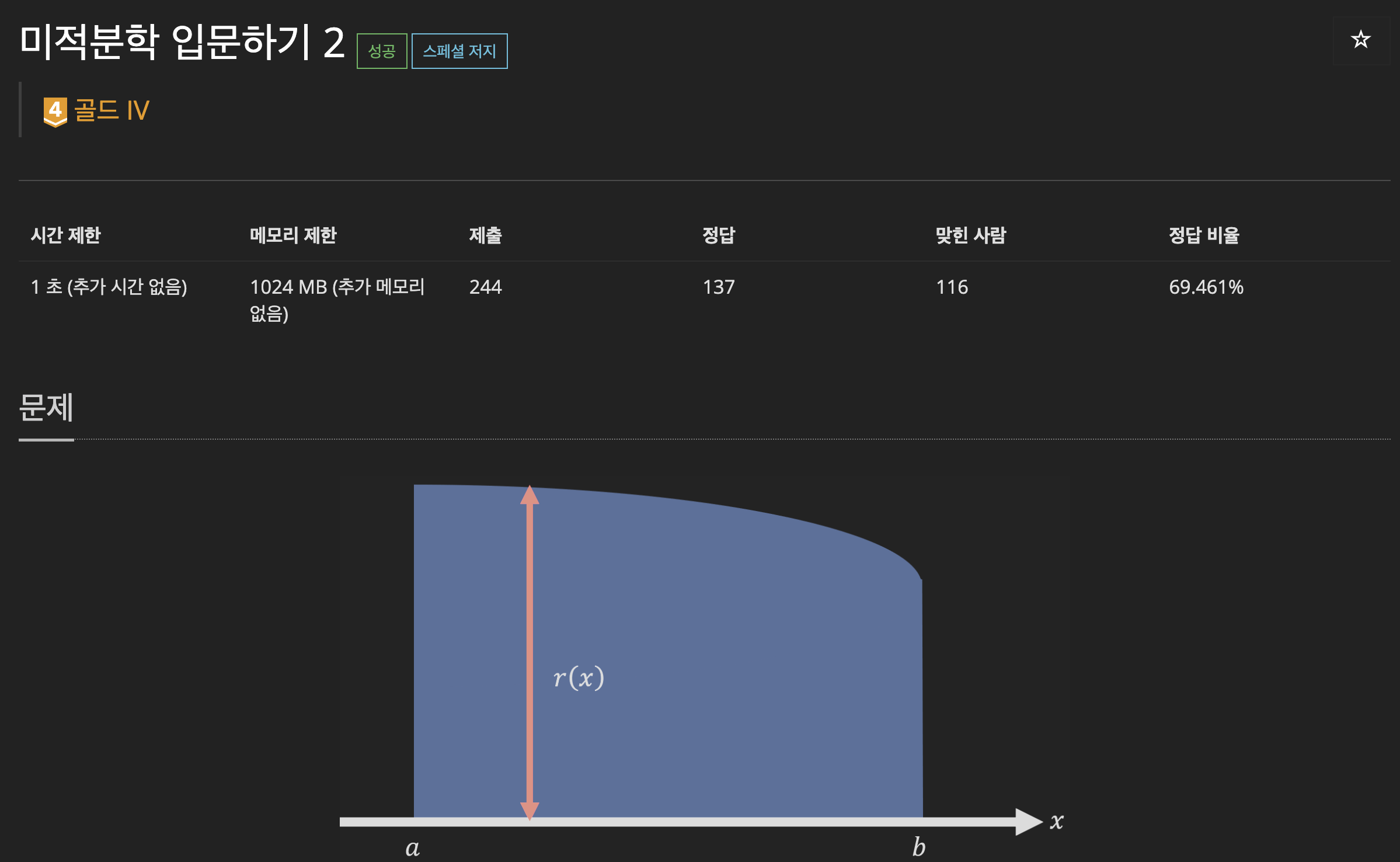
파푸스-굴딘 정리를 이용해서 구할 수 있다.

평면 도형의 무게중심 $G$와 평면 도형의 넓이 $S$를 안다면

도형과 완전히 접하거나 떨어져있는 축으로 회전했을 때 생기는 부피 $V$는

축과 무게중심의 거리가 $d$라고 할 때,

$V=2 \pi dS$ 이다.

double tri_area(pair<T, T> a, pair<T, T> b, pair<T, T> c) {
   return 0.5 * abs((a.x * b.y + b.x * c.y + c.x * a.y - b.x * a.y - c.x * b.y - a.x * c.y));
}

void solve() {
   pd a, b, c;
   cin >> a.x >> a.y >> b.x >> b.y >> c.x >> c.y;
   double area = tri_area(a, b, c);
   double gx = (a.x + b.x + c.x) / 3;
   double gy = (a.y + b.y + c.y) / 3;

   double v = area * 2 * PI * gy;
   cout << setprecision(9) << fixed << v << ' ';
   v = area * 2 * PI * gx;
   cout << setprecision(9) << fixed << v ;
}