BOJ 21099 - Four XOR

BOJ 21099 - Four XOR

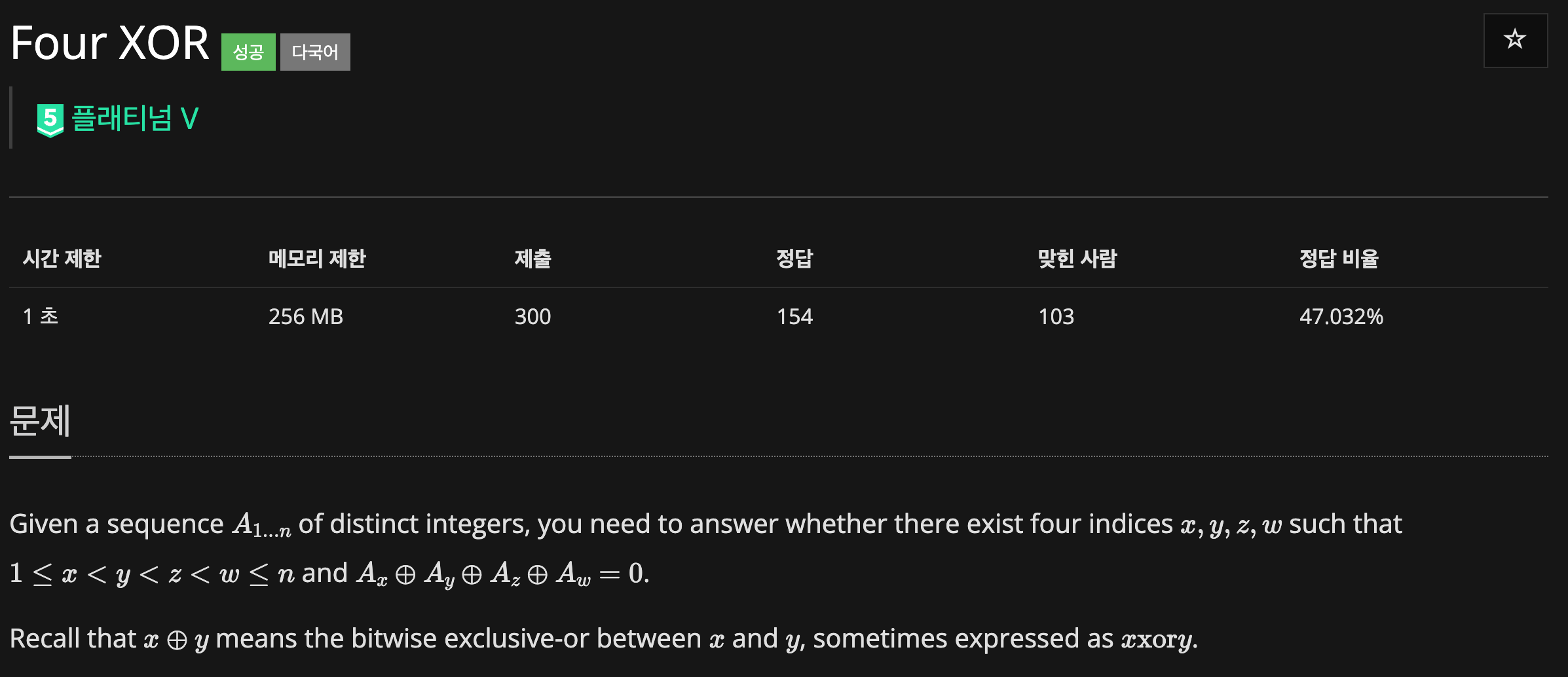
30분동안 낚인 문제

$n$이 충분히 크다면 $A_i$를 비둘기집의 원리에 의해 어떤 수로 구성하든 $0$이 항상 만들어진다는 것이 핵심이다.

$A_x \oplus A_y \ne A_z \oplus A_w$ 가 되기 위해선, $A_x \oplus A_y$ 의 가지수를 생각해보자.

모든 수가 다르므로 대략 $O(n^2)$ 가지이다.

$A_x$ 가 가만히 있고 $A_y$ 의 후보들에 대해서 $A_x \oplus A_{y'} = A_x \oplus A_y$ 가 나올 순 없다. 또한, 그렇다고 $A_x$를 바꿔서 $A_{x'} \oplus A_{y'} = A_x \oplus A_y$ 가 나오게 하면 애초에 $4$가지의 수로 $0$을 만들어버리는 경우이므로 피해져야 한다.

그런데 $A_z \oplus A_w$ 는 모두 이 수와 달라야 하는데 이것도 $O(n^2)$ 인데, 그럼 결국 $O \left( \dfrac {n(n+1)}2 \right) < \dfrac {100,000}2$ 가 되야 한다는 의미이다.

실제로 $n > 350$ 에 대해 그냥 Yes를 출력하는 코드가 통과했다.

적절한 $n$을 설정하여 그 위는 항상 Yes 이고, 그 밑은 완전탐색을 해줄 수 있다.