BOJ 10121 - Salad Bar

BOJ 10121 - Salad Bar

스택을 잘 이해해야 풀 수 있는 문제이다.

풀땐 세그먼트 트리도 같이 썼는데, 스택만 써서 $O(N)$풀이를 한 번 고안해보도록 하자.

---

$a_i$를 $s_i=p$ 라면 $1$이고 아니라면 $-1$을 한 것의 현재까지의 합이라고 하자.

그리고 $b_i$ $i$에서 왼쪽에 있는 정답 구간 $(b_i, i]$ 라고 하자. 즉, $i$에서의 정답은 $i-b_i$ 이다.

이건 그걸 사진으로 나타낸 것이다.

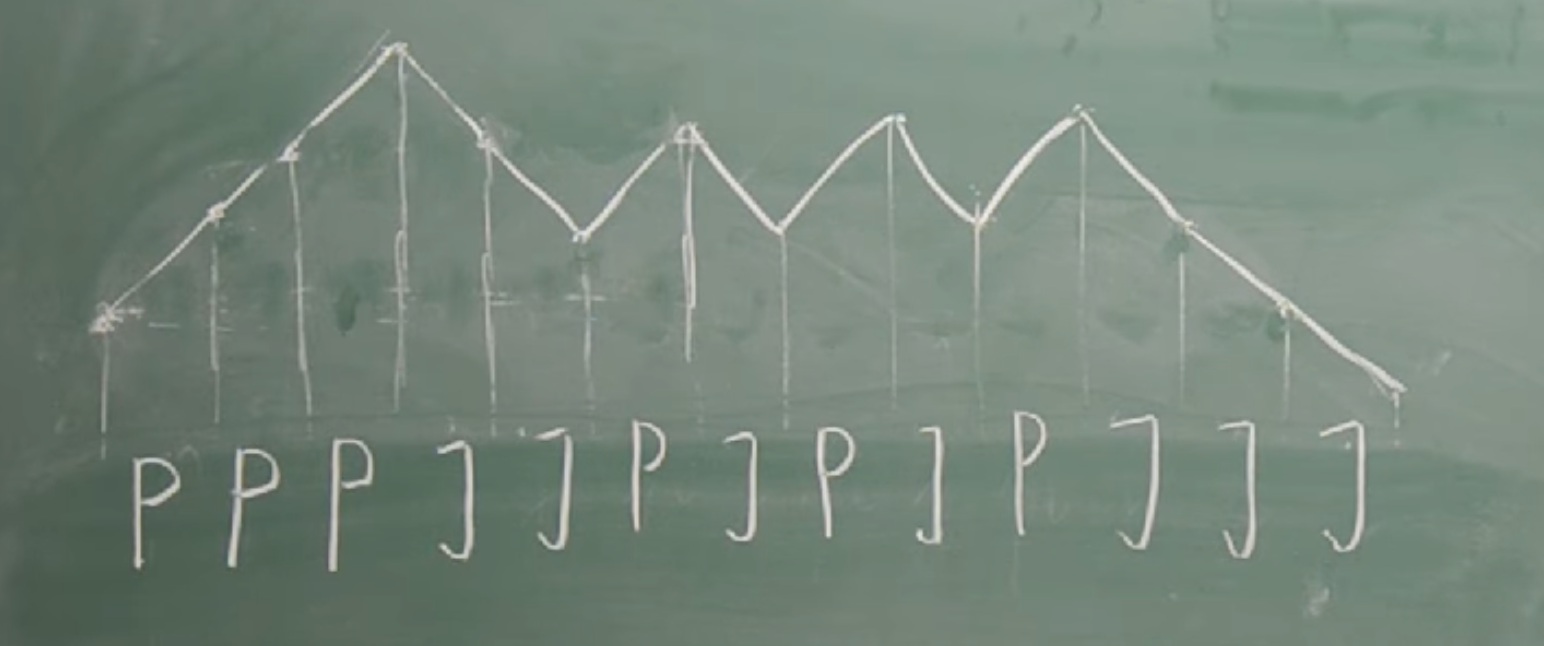
https://www.youtube.com/watch?v=iOjJq_M47rU&ab_channel=OlimpiadaInformatyczna

int cur = 1e9;  
int idx = 0;  
int ans = 0;  
for (int i = 0; i <= n; i++) {  
   while (sz(v) && a[v.back().fi] > a[i])  // 1
      v.pop_back();  
   int idx = i;  
   while (sz(v) && v.back().se <= a[i]) {  // 2
      idx = v.back().first;  
      v.pop_back();  
   }  
   ans = max(ans, i - idx);  
   v.push_back(make_pair(idx, a[i]));  
}

스택에 $(b_i, a_i)$ 를 관리하는데, $a_{b_i}$는 비감소하고 $a_i$는 단조감소하게 관리하자.

$b_j \cdots j \cdots i$가 있을 때, $(b_j, j)$ 구간은 정답으로 가능하므로 $[j, i]$ 만 정답으로 가능하면 $(b_j, i]$ 도 가능하다.

따라서 $2$처럼 가능한 정답 $(b_j, j)$가 있다면 $b_i \coloneqq b_j$ 를 해주고 $(b_j, i)$ 처럼 정답을 확장시키면서 계속 pop 한다.

$a_j \le a_i$ 라는 것은 $j \leftarrow i$로 이동할 수 있다는 뜻이다.

그리고 $1$에서는 $b_j \to i$ 로 이동할 수 없는 것들을 모두 삭제한다.

$1$에서 pop을 해도 되는 이유는 어차피 이후에 볼 $i'$ 들은 $i < i'$ 라서 $b_j \to i$가 안되면 $b_j \to i'$도 안되기 때문이다.

따라서 이렇게 갱신하면 $b_j \to i$ 와 $i \to b_j$ 가 가능해지기 때문에 이 구간을 정답이라고 볼 수 있다.