Bellman Ford Shortest Path
Bellman-Ford Shortest path
벨만-포드 최단경로 알고리즘은 $O(VE)$에 그래프에서의 최단 경로를 찾을 수 있는 알고리즘이다.
어떤 시작 지점 $S$ 에서 다른 모든 정점까지의 최단 거리를 구해준다.
다익스트라 알고리즘만으로도 $O(E\log V)$ 의 시간복잡도로 구현을 할 수 있는데 벨만-포드 알고리즘은 왜 필요할까?
벨만 포드 알고리즘은 간선에 음의 가중치가 있을 때도 최단 경로를 찾을 수 있기 때문이다.
음의 가중치라는건 다음과 같은 경우를 의미한다.
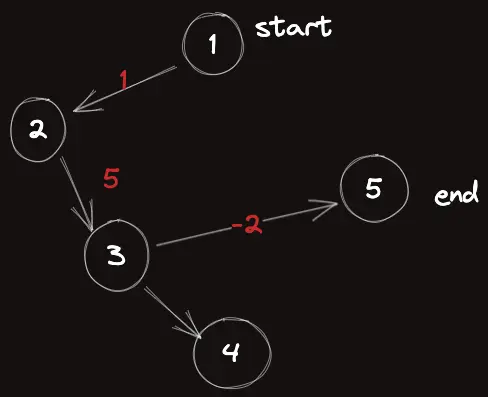
start 부터 end 까지 최단 경로는 6-2=4 이다.
그런데 이 경우 다익스트라 알고리즘을 돌려도 동일하게 4가 잘 찾아질 것이다. 그럼 벨만-포드 알고리즘은 쓸모가 없는 것일까?
벨만-포드 알고리즘의 진가는 싸이클 중, 돌 때마다 최단 경로가 줄어드는 싸이클이 있는지를 검출할 때 드러난다. 이를 음의 가중치 싸이클이라고도 한다.
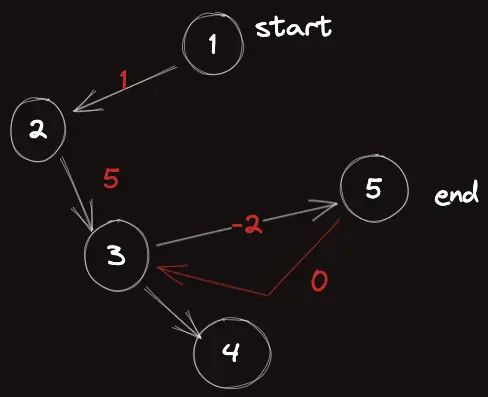
빨간색 간선이 생긴다고 하면, 3번 노드는 계속해서 방문되게 된다. 왜냐? $3 \to5 \to 3$ 를 반복하기만 하면 최단 거리가 $2$ 씩 계속해서 줄어들기 때문이다.
이러한 경우 start부터 end까지의 최단 경로는 $-\infty$ 가 되며 이 경우 “최단 경로를 구할 수 없다.” 라고 해야 옳다.
음의 싸이클 가중치의 존재와 $u \to v$ 로 가는 최단경로를 구할 수 없다는 동치가 아니다. 밑에 내용에서 설명할 것이다.
벨만-포드 알고리즘은 이러한 경우까지 처리할 수 있고, 음의 가중치 싸이클의 유무까지 검출해낼 수 있는 알고리즘이다.
어떻게 동작하는지 살펴보자.
알고리즘
$E$ 개의 그래프에 존재하는 모든 간선들을 다 보는데 $O(E)$ 가 걸리고 그걸 $V$ 번 반복한다고 해보자.
벨만-포드 알고리즘은 위와 같이 동작하는데, 대략 다음과 같다.
for(int v = 1; v <= V; v++){ // V 번
for(int i = 0 ; i < V; i++){ // V 번
for(Edge e: E[i]){ // i 번째 노드의 간선 개수 만큼
...
}
}
}
대략적인 for문을 보면 이것의 시간 복잡도가 $O(VE)$ 인지 착각하기 쉽지만, 결국 모든 $E$ 에 대해서 한 번의 가장 바깥쪽 for 문에서 한 번씩만 거치기 때문에 올바르다.
$V$ 번의 시도동안 각 간선 $e$ 들에 대해서 해주어야 할 것은 다음과 같다.
$e{:}~u\to v$ 이고 가중치 $w$ 를 가진다고 할 때, $u$ 가 한 번이라도 도달된 적이 있는 상태라면, $\Large D_v=Min(D_u+w,\,D_v)$ 를 해준다.
이를 edge relaxtion이라고 한다.
이 과정을 모든 $e$ 에 대해 $V-1$ 번 반복하게되면 무조건 $\rm start \to end$ 로 가는 최단 경로가 찾아진다. 왜냐면 $\rm start \to end$ 까지의 최단경로의 최대 간선수는 $V-1$ 이기 때문이다.
그렇지 않다고 하면 어떤 정점을 두 번 이상 거친다는 의미인데, 그러려면 음의 싸이클이 있다는 의미이므로 최단 경로라는 것이 의미가 없어지기 때문이다.
이상한 점을 느꼈는가? $V-1$ 번만에 찾아지는데 왜 제일 바깥쪽 for 문은 $V$ 번을 시행했을까?
이것이 바로 음의 싸이클을 검출하는 핵심이다.
만약 $V-1$ 번 이후의 edge relaxtion시도에서 최단경로가 단축되는 정점이 있다면 그것은 곧 음의 싸이클이 존재한다는 것을 의미하게 된다.
구현
BOJ 11657 - 타임머신 문제를 풀어보도록 하자.
$1 \le N \le 500$ $1 \le M \le 6,000$
이므로 $O(VE)$ 는 벨만-포드 알고리즘으로 충분히 시간안에 돌 수 있다.
다음과 같은 조건을 보자
만약 1번 도시에서 출발해 어떤 도시로 가는 과정에서 시간을 무한히 오래 전으로 되돌릴 수 있다면 첫째 줄에 -1을 출력한다.
이것이 바로 벨만-포드 알고리즘을 써서 음의 가중치 싸이클의 존재 유무를 찾으라는 문구이다.
다음과 같이 풀 수 있다.
int V, E;
cin >> V >> E;
vector<vector<pi>> edges(V);
while (E--) {
int u, v, w;
cin >> u >> v >> w;
u--, v--;
edges[u].pb({v, w});
}
vi dist(V, 1e15);
dist[0] = 0;
bool neg_cycle = 0;
for (int t = 1; t <= V; t++) {
for (int i = 0; i < V; i++) {
if (dist[i] == 1e15) continue;
for (const auto&[to, w]: edges[i]) {
if (dist[to] > dist[i] + w) {
if (t == V) neg_cycle = 1;
dist[to] = dist[i] + w;
}
}
}
}
if (neg_cycle) {
cout << -1;
} else {
for (int i = 1; i < V; i++) {
cout << (dist[i] == 1e15 ? -1 : dist[i]) << endl;
}
}
이 블로그의 글은 가끔 int 를 써도 long long을 의미할 수도 있다. 이건 필자가 #define int long long 같은 템플릿을 쓰기 때문인데, 이러한 부분들을 고려하면 된다.
주의해야 할 것
벨만-포드를 이용하는 문제에서 무엇을 요구하는지를 잘 파악해야 한다.
크게 두 가지가 있을 수 있다.
- 음의 가중치의 존재의 유무를 구하라
- 음의 가중치의 존재를 구하고 그것 때문에 $\rm start \to end$ 까지의 경로에서 최단 경로를 찾을 수 없는지 구하라
위 두개는 다른 말이다. 두 번째 조건은 첫 번째 조건을 포함하지만, $\rm start \to end$ 까지의 경로에 그 싸이클이 포함되는지까지 검사를 해주어야 한다.
예를 들어, 음의 싸이클이 존재해도 그 경로에 존재하지 않으면 최단 경로는 존재하기 때문이다.
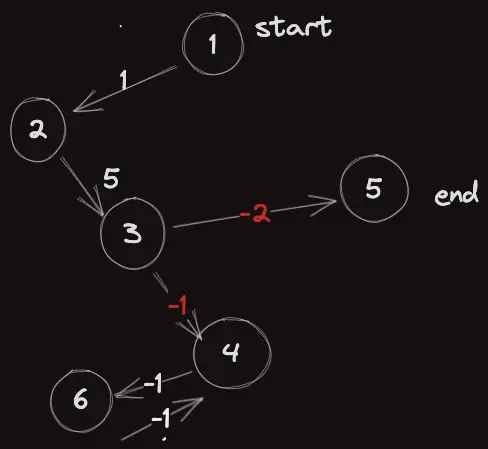
위 그래프를 보면 $4 \to 6 \to 4$ 같이 음의 싸이클이 생겨 계속해서 거리가 줄어들지만, $1 \to 2 \to 3 \to 5$ 까지 가는 경로에 저 싸이클이 포함될 수 없기 때문에 최단 경로는 구해진다.


Comments