0-1 Segment Tree
Prerequisite
- Segment Tree
0-1 Segment Tree
0-1 Segment Tree란 이름은 내가 지은 이름인데, 일반적인 세그먼트 트리에서 구간에 대해 합을 구할 수 있는것에 비해 이 세그먼트 트리는 전체 구간에서 0이 아닌 구간의 개수를 세준다.
보통 이 트리는 스위핑 알고리즘과 같이 쓰인다.
쿼리가 전체 구간에서만 가능하다.
이렇게 세그먼트 트리를 구성하면 구간이 몇번 중복되어 더해져 값이 1이상일 수 있지만, 1이상인 값들의 개수를 셀 때 쓸 수 있다.
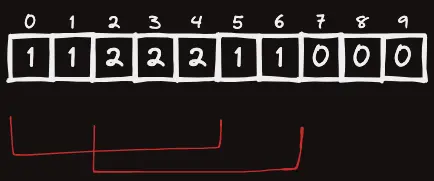
빨간 구간에 1씩 더하는 연산을 했을 때, 우린 $[0,\,9]$에 쿼리를 날리면 1이상의 값이 있는 칸의 개수인 7을 얻고 싶은 것이다.
또한 이 자료구조는 구간에 대한 업데이트를 할 수 있다
시간복잡도는 $O(\log N)$ 이고, 전체 구간에 대한 쿼리에 대한 시간복잡도는 $O(1)$ 이다.
주의할 점
이 트리는 일반적인 세그먼트 트리와 동작 방식이 조금 다르기 때문에 절대적으로 주의해야 할 사항들이 있다.
전체 구간에 대해서만 쿼리가 가능하다.
즉, 세그먼트 트리의 크기를 $N$ 으로 잡았다면 항상 $0 \sim N-1$ 의 구간만 쿼리가 가능하다는 것이다.
이 쿼리는 $O(1)$에 가능하다.
동일한 구간에 대해서는 우선적으로 $+1$ 을 해야한다.
$[2,3]$ 에 $+1$ 업데이트를 했다면 추후에 더이상 트리가 필요없지 않는 이상 $[2,3]$ 에 $-1$ 업데이트가 되는 방식으로 트리를 사용해야 한다.
예를 들어, 구간의 길이가 $5$라면 $[0,4]$ 에 $+1$ 을 해준다음 $[3,3]$ 에 $-1$ 을 해주는 것 같은 쿼리를 날릴 수 없다.
왜인지 정확히 모르겠다. 사실 이 명제가 제대로 된건지도 모르겠고, 그냥 이걸 이용해 문제를 풀다가 왜안되지 하고 알아낸 사실이다. 아시는 분 제발 알려주세요
관련된 글을 코포 댓글 D 해설에서 찾을 수 있었다.
구현
구현은 세그먼트 트리와 크게 다르지 않다. 특히 쿼리는 아예 동일하게 날릴 수 있다.
$tree$ 라는 변수는 구간을 모두 변경시켜줘야 할 때만 더해준 $\sum$ 을, $len$ 이라는 변수는 $0{-}1$ 연산에 맞는 구간합을 가지고 있다고 하자.
이 글에서 1이상인 구간을 세는 연산을 $0{-}1$ 연산이라고 하겠다.
template<class T>
struct seg_tree_01 {
int N;
vector<T> tree;
vi len;
seg_tree_01(int N) : N(N) {
int tree_size = 1 << ((int) ceil(log2(N)) + 1);
tree.resize(tree_size);
len.resize(tree_size);
}
void update(int n, int nl, int nr, int l, int r, T v) {
???
}
T query() { return len[1]; }
void update(int l, int r, T v) { update(1, 0, N - 1, l, r, v); }
};
쿼리부분에서 결국 반환해주는 값이 $len$ 이므로 쿼리에서 $0{-}1$ 연산의 결과를 반환함을 알 수 있다.
그럼 이제 update 부분만 어떻게 실행되면 되는지 생각해보자.
void update(int n, int nl, int nr, int l, int r, T v) {
if (nr < l || nl > r) return;
if (nl >= l && nr <= r) {
tree[n] += v;
} else {
int m = (nl + nr) >> 1;
update(n * 2, nl, m, l, r, v);
update(n * 2 + 1, m + 1, nr, l, r, v);
}
if (tree[n] > 0) len[n] = nr - nl + 1;
else if (nl == nr) len[n] = 0;
else len[n] = len[n * 2] + len[n * 2 + 1];
}
일단 기본 구간합 세그먼트 트리처럼 $tree$ 에 대한 합을 계속해서 더해줘야한다.
그런데 특이하게도, 항상 $[nl,\,nr]$ 이 $[l,\,r]$ 구간에 완전히 포함될 때만 $tree$ 를 업데이트 시켜주고, 그 경우 자식의 트리를 업데이트 하지 않음을 알 수 있다.
이렇게 저장을 해야 $len$ 을 올바르게 업데이트시켜줄 수 있기 때문이다.
이제 $len$을 업데이트 하는과정을 보자.
- $tree_n$ 에 값이 존재한다면 이 구간의 $0{-}1$ 값은 세그먼트 트리에서 정점이 의미하는 값 그 자체$(=nr-nl+1)$이다.
- 만약 leaf 노드이고 $tree_n=0$ 이라면 $len_n=0$ 이다.
- 그렇지 않다면 $len_n=len_{\rm left}+len_{\rm right}$ 이다.
왜 이것이 올바른지 조금 더 살펴보자.
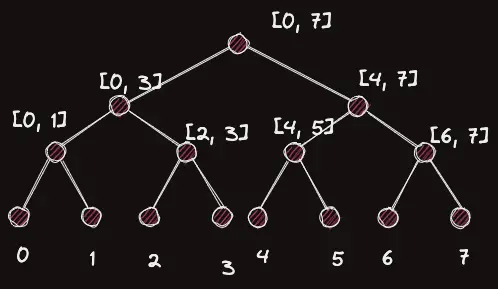
$[0,\,3]$ 에 1씩 더해준다고 하자.
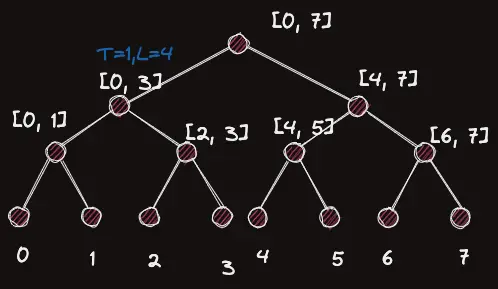
그럼 이렇게 $[0,~3]$ 노드에 $tree=1$ 이고 $len=3$ 으로 업데이트 된다. (루트 노드의 업데이트는 생략했다.)
그럼 이제 전체 구간에서 1이상인 칸의 개수는 $len_{root}$ 가 4로 업데이트가 되어 있을 것이므로 $4$ 라고 $O(1)$에 구해줄 수 있다.
좌표 압축
이 세그먼트 트리에서 유독 좌표압축까지 해야하는 문제들을 몇개 본거같은데, 좌표압축은 다음과 같이 한다.
$[l, r]$ 범위에 대한 어떤 것들을 존재하는 value 값으로 모아둘 때, $l, r$과 함께 $l-1$ 도 같이 모은다.
이제 $[l, r]$ 범위에 대한 업데이트에 대해 두 가지 경우가 나뉠 수 있다.
- 문제에서 다루는 좌표가 점을 의미해서 구간의 길이를 구하는 경우 (아래 7626 문제)
- 문제에서 다루는 좌표가 칸을 의미할 때 (아래 25447 문제)
$1$은 보통 $[l+1, r]$ 을 업데이트하고 트리 내부에서
len[n] = compressed[nr] - compressed[nl - 1]; 다음과 같이 코드만 다르게 쓴다.
이렇게하면 범위 $nl \sim nr$을 관장하는 노드 $n$이 정확히 그 구간을 의미하게 된다.
$2$는 보통 $[l, r]$ 을 업데이트하고 트리 내부에서
len[n] = compressed[nr] - compressed[nl - 1] 을 쓰자.
우린 $l-1$ 을 넣어두었기 때문에 이것이 동작한다.
연습 문제
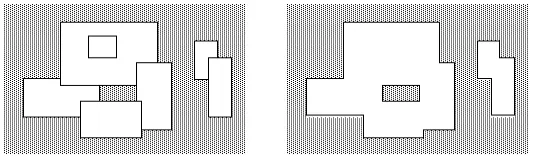
이 문제는 0-1 세그먼트 트리를 이용해 풀어줄 수 있다.
일반성을 잃지않고 가로로 sweep하는 경우를 보자.
각각의 직사각형에 대해 $(x_1,y_1,y_2,z)$ 와 같은 event 객체를 두 개씩 만든다.
직사각형이 삽입될 때의 $z$는 $z=-1$, 제거될 때의 $z$ 는 $z=1$ 이다.
삽입될 때가 정렬순으로 더 빨리 오게 하기 위함이다.
이제 저 $x$ 에 대한 오름차순, $x$가 같다면 $z$에 대한 오름차순으로 정렬하고 스위핑한다.
이제 계속 vertical line들을 더해주고 빼주면서 그직전 값들과 차이를 계속해서 정답에 더해주면 된다.
좌표압축이다. 위 문제들과 비슷하게 푼다.
DFS를 돌리며 이 세그먼트 트리를 써서 좌표압축까지 해서 풀어야 한다.
Comments